Extrapolation and interpretation of data
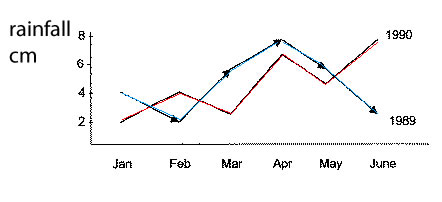
We do not only have to construct proper graphs but we must also be able to interpret and use the data represented by them.

Consider the graph on the right. It shows the rainfall during several months of the year.

a) How much rain fell in April of 1989?

b) What is the difference between the rainfall in Feb of 1990 and Feb of 1989?

c) Which year had the greatest total rainfall for the period of time shown?

d) Which is the wettest month on the graph?

e) Identify the independent and dependent variable.
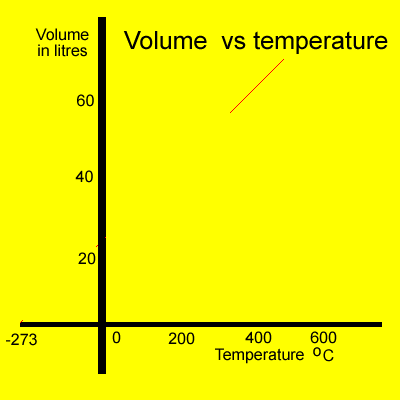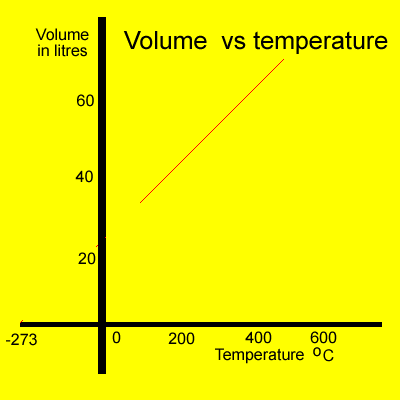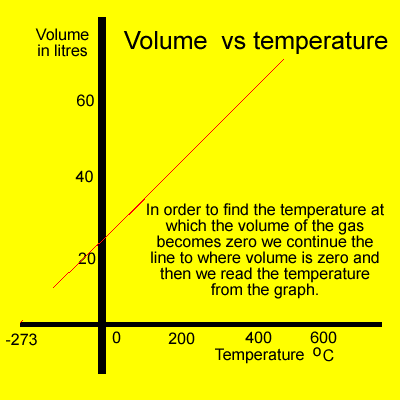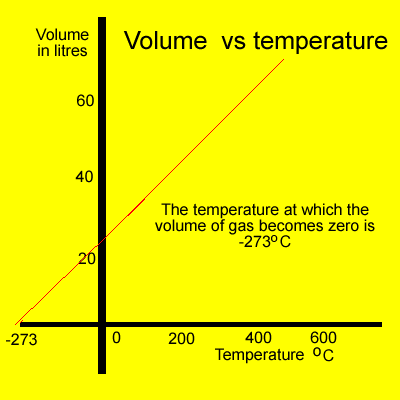
Suppose we measured the volume of a gas at different temperatures ranging from 100oC to 0oC . At 0oC the volume was 22.4 litres. How can we use the graph to find the temperature when the volume of the gas becomes zero?
We simply extend the graph to where the volume is zero. In other words we continue the graph to the x-axis and read the temperature at the point where the graph intersects the x-axis, as shown below.
The temperature at which the volume of the gas becomes zero is -273oC. Predicting a value outside the data is called extrapolation. In this case we extended the graph, based on its previous shape to predict the temperature at which gas has zero volume.

Several solutions of glucose were tested to see how much light of a particular wavelength they each absorbed. The results are presented in the table below.

Glucose concentration (g/ml)
Absorbance(absorbance units)
0.000
0.000
0.005
0.100
0.010
0.190
0.015
0.285
0.020
0.375

On the set of axis provided below, plot a graph of absorbance versus concentration.
A sample of unknown glucose concentration was analysed and was found to have an absorbance reading of 0.480. What is the glucose concentration of this solution.
Another solution of glucose had an absorbance reading of 0.550. What is the glucose concentration of this solution?
Solution
Continue with interpreting data.
Chalk Vinegar